脳の健康管理、あなたの将来は大丈夫ですか？

＜学徒の魂、百まで＞
今年の遅れ馳せながらの桜よりピカピカのフレッシュマンに目が注がれます。

どうぞ中学や高校とは指導法がどんなに違うか、お楽しみアレ～　？


グローバル化の速度はあらゆる分野で著しいものがあります。とはいうものの私達の脳は生まれ育った日本という環境や文化、いえ、親の背、教師の背に負う所が多分です。

ですからそう簡単には自分作りや先を読む能力は得られませんね。大波を超えるための人生に必要な技は時を越えて自分で磨くしかありません。

大波といえば危なげなユーロ圏の経済ニュースがいつもどこかに登場です。今にも私たちを飲み込みそうな大波が続いています。

ユーロ圏では新たな経済世界を目指すとともに経済のツールである通貨もカラフルなユーロ紙幣に替わりました。

かつてのドイツのマルク紙幣は確率分布曲線（本ブログ）とその発見者のガウス（1777-1855、独逸）の顔が載っている荘重なものでした。

ものごころが付いた頃からお札を使うたびにガウスと向き合うわけです。

確率的な思考に満ちた人生であることでしょうね。

＜確率密度曲線と区間推定＞
ガウスの時代の数学者達は、現実にはデータが取りきれないような母集団の特性を把握するための数学的解析法を求めて統計学を発展させました。

さて人々の身長の分布や工場製品のばらつきについて分布を調べると標本サイズを上げるほどに、得られた標本値の分布は平均値の付近に集積します。そして左右対称の釣鐘型となる正規分布という分布型に近づきます。

ガウスは母集団の特性を知るためにはほぼ３０以上の抽出サンプルがあると平均値（μ）と標準偏差（σ）を用いた関数式によってその母集団の分布曲線に近似できることを示しました。
その関数式は確率密度関数式（本ブログ）と言い、積分すると、すなわちx軸（確率変数）と曲線で囲まれた面積が１となります。

さてこの発見はどのように世の中に役立つのでしょう。

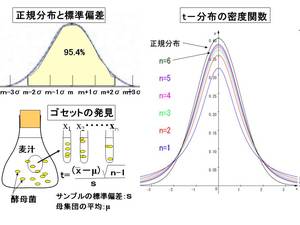図の左上が示すことはデータが±１σの範囲に入る確率は約６８．３％、±２σでは９５．４％、の確率であることを意味します。
平均値（μ）や標準偏差（σ）がどんな値であっても±１σや±２σ、±３σの範囲に入る確率は常に一定に、０．６８３、０．９５４、０．９９７となるのです。ですから平均値と標準偏差の値と目的のデータを比較すれば自ずと全体の中での特性が分かります。

しかしサンプルがヒトの場合や販売品は沢山の標本数を取って調べることが出来ません。
そこではt－分布を用いたt検定法が使われます。

＜ｔ－分布とStudent‘s t-test＞
化学と数学を学んだゴセット（1876-1937英国）はビール会社ギネスに就職しました。ギネスブックで有名ですね。

彼は醸造所で味が一定の良いビールを作るために日夜、タンクの中から酵母菌の入った麦汁を少し取り出しその菌の数を数えてタンクのビールの出来具合を推定していました（図の左下）。

製品管理のためのこの仕事において、ガウスの言うように何回も測定頻度を重ねれば一定の値により近づき、タンクの酵母菌濃度とブレが少なくすむ、ということは分かっていました、がゴセットはもっと少ない抽出実験でより正しく調べることが出来ないものか、と考えたのです。

そこで発見したのがt－分布という確率分布です。これは標本数を増やすとガウスの正規分布に近づきます（図右）。
ｔ－分布は少ない標本のみで母平均を推定することが出来るのですから凄い発見でした。

またｔ－分布を使うと２つの母集団からの２つの標本平均の差がどういう確率で有意となるか、という検定が出来ます。いわゆるStudentのｔ－テストと呼ばれる検定法です。

私たちが実験結果の報告をする時はデータをStudent のｔ-testを用いて解析した、と記し（参考）危険率が0.001（参考論文の場合）で両群のデータの平均に差があるといえる、のように確率Pがどの位小さかったかを記します。これによって読者はどれくらい危なっかしい、あるいは信憑性が高い研究結果なのかが判断出来るわけです。

Student’s t-testではunpaired　ｔ－test　としても記します。この時は対応がない独立な二つのデータにおいて平均に違いがあるかどうかを知るための検定です。

ところで　‘Student’ はゴセットのペンネームです。"学生”としたのが謙虚でいいですね～"脳研究者”などと書かない・・・

自分が出したデータを説得したい側としてはエクセル分析ツールでまずF検定を行います。そこでは比較したい両データの分散のばらつき具合を検定します。ある決められた確率で分散が等しいと判定されると、その次にｔ検定をクリックしてその中の分散が等しいと仮定した場合を、あるいは等しくない時は、等しくないと仮定した場合を選び検定結果の表と危険率P値を得ます。

なおpaired t-test(対応がある)、をエクセルで選ぶ場合は、例えば薬の投与効果を検定したい場合など、即ちbefore and afterで効果の有意差検定をしたい時です。投与前後のデータをセルに挿入後、危険率を得ます（参考、論文中図１の説明文）。

＜現代社会に必要な統計学＞
母集団の分布型がおよそ分かっている多くの生物や物理の現象や物質の特性は正規分布やt－分布の関数式によって確率論的に解析が出来ます。

ところが企業の戦略としては経済の動きや人々の購買意欲に関する全体像の解析がとても重要です。また資源の乏しい日本は他国からの物資の仕入れに関する戦略が生き残りに関わります、またIT情報の篩い操作など、これらは確率分布が決められないものですが必須のニーズとなっています。

でもこれらは次に起こることによって確率が変わりますので関数は得られないのです。

では現実社会の諸問題に統計学は太刀打ち出来ないのでしょうか。

要因が多すぎるから誰かの勘に頼るしかないのでしょうか？

現在は医療診断システムや、インターネットで受信したものがスパムメールである確率の計算などは社会数学ともいえるベイズの理論モデルを使って、不完全情報下での解析として進められています。

何はともあれ、何を調べたいのか、いかなる質と量のデータを得ればよいのか、そして分布の様式がどうなのかなど、判断が得られるような適切な分析法を進めていくことが重要です。

　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　
　　　「庭の桜はまだちらほらだね。

　　　次のブログでは桜の花がアップされるかな～」