脳の健康管理、あなたの将来は大丈夫ですか？

＜要因が複数ある時の統計解析はーー＞
FTESTのFはF検定のFジャン～

というだけではないのです。

Fは統計学の父、フィッシャー（1890-1962,英）のFです。

数学と生物学を学んだフィシャーは、ロンドン郊外の農事試験場に就職しました。

広大な敷地にある質や環境が異なる畑では同じ植物でも生育が異なり、肥料の効果もはっきり攫めません。要因が沢山あって答えが出せないのです。

さてｔ-検定を使えば、２群の平均値に差があるといえるか、という検定はできます（本ブログ）。
そこでフィシャーはそれを広げて複数のグループ間の要因に違いがあるかどうか調べられないか、と探求しました。

そして群間分散/郡内分散を調べて群間に差があることが有意かどうか、がわかる検定法を発見しました。分散分析（ＡＮＯＶＡ）です。

データが左上の表のような場合は、エクセルの分析ツールの「二元配置のくり返しのない分散分析」を選びます。
次にデータを囲んで分散分析表を得ます。
有意水準を５％とするならその表のＰ値から、各畑においては有意に、状態の違いがある、と言えることがわかるのです。

すなわち分散分析は分散の比の検定を行って要因によっておこる変動が誤差内かどうかを調べているのです。


復習となりますがｔ－検定には３種類あってどれを使うかは、まずＦ検定を行うことによって、与えられた二群のデータが等分散か不等分散かを決めました。それから分析ツールの中の適切なｔ－検定を選択して解析しました。

正規分布では確率密度曲線を描くのにNORMDISTの関数値を使いました(本ブログ）。また、ｔ-検定ではTTESTの関数式よりＰ値を得ました。

さてF検定でもエクセルに関数が揃っています。
FTEST（両側確率Ｐ）やFDIST（片側確率Ｐ）、FINVという関数を使ってＦ分布上のＰ値やＦ値が求められます。

このＦ分布という分散比の確率分布を用いたＦ検定と分散分析の発見こそフィッシャーの偉業とされているものです。

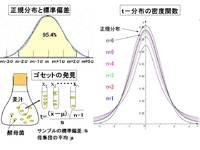
＜Ｆ分布の確率密度曲線＞
ところでＦ分布という確率分布は正規分布（本ブログ）やｔ-分布（本ブログ）の確率分布と違ってそのグラフは自由度によって大きく変わり左右対称でないのが特徴です。

その確率密度を出す関数式がエクセルではアドインされていません。
そこで私はNTFDISTという関数をエクセルに組み込みました。

ここでは自由度が３と４、３と１０の値を使ってNTFDIST関数による２種類の確率密度の値を出しました。そして散布図をクリックしてＦ分布のグラフを作成しました（図の右上）。

＜品質管理と分散分析＞
分散分析は育種や研究開発などにおける実験結果の分析のみではありません。
「世界一の品質を持つ日本！」と言われるように日本製品における品質管理では統計学が力を発揮しています。

統計的品質管理に卓越するには、数々の要因の中から品質に影響をおよぼす異常原因を統計学的に見つけ出す、そしてきちんと対処する、これに尽きますね。

このように分散分析は統計的現象の原因究明やグループ間の要因解析ができるので複数の患者への薬の効果を調べる場合にもうってつけです。

要因がひとつである一元配置の分散分析の例としては、結核菌の再来を抑えるべくしてなされた下記のようなスクリーニングの研究報告があります。

＜多剤耐性結核菌を撲滅するには＞
先日も結核菌集団罹患のニュースがありました。

日本は先進国の中でとても結核罹患率が高いのです。

なぜこの現代に結核菌に脅かされるのでしょう。

戦後、結核は日本の死亡原因の第一位でしたが化学薬品のお陰で非常に減りました。

ところが中途半端な化学療法によって耐性結核菌が生じてしまったのです。対処に困難を極めています。

南アフリカでは結核やＨＩＶに効くとされる植物由来の民間薬が沢山あるそうです。しかしその科学的な検証はなされていません。

論文では２１種類のうち４つの植物で結核菌と薬剤耐性菌の増殖を抑えることが解析されました（参考）。

成分の抽出とさらなるバイオアッセイを進めて薬剤耐性菌に効く天然の成分が分かると良いですね。

なにはともあれ結核菌に冒されても薬効が得られて死なずに済むように、薬の併用や免疫力の低下を個人のレベルで防いでおくことが大切です。

日々の健康管理に勝るものは無し、です～