脳の健康管理、あなたの将来は大丈夫ですか？

上記の広告は、60日以上更新がないブログに表示されています。
新たに記事を投稿することで、広告を消すことができます。  

＜ゼロは満ち足りた世界！＞
数年前、私はテレビでの邦画"博士が愛した数式”の公開ＣＭに思わず目が注がれました。

主人公である老数学者は、なんと若かりし頃（私も）に、私が愛した？「ルビーの指環」を自ら作曲して歌って一斉を風靡した歌手だったのです。

老数学者は交通事故に遭って、記憶が数十分しか持ちません。しかしオイラーの公式は決して忘れません。

オイラー(1707-1783,スイス)の公式（図、左上）は物理学者のファインマン（1918-1988,米）に“our jewel”と言わしめた美しい数式です。

博士は身近のひとびとをオイラーの等式(図、左上)の文字になぞらえます。それらは無限の小数である無理数と虚数です。

自然対数の底である自分（e）の肩に乗る母屋に住む不倫相手（虚数、i）、そこに加わる家政婦（パイ、π）、ぎこちない空気です。

ある日、家政婦の子供のルートという少年（＋１）が現れて博士の心は少年と通うようになります。

博士はルート君が来て、オイラーの公式が自分がこよなく愛するゼロになった、とオイラーの公式でθがπになった時の等式（図、左上）に幸せを感じるのでした。

＜エクセルで描くオイラーの公式＞
オイラーの公式におけるθの単位はラジアンです。

公式でθが家政婦のπになった時の右辺の計算は、三角関数を勉強中の高校生以外はsinπやcosπの値がすぐ出てこないかもしれません。

心配ご無用です！エクセルなら最初のセルに＝RADIANS(A2)として下方にドラッグすれば度からラジアンへ変換されます。
三角関数の値はC2のセルに＝COS（B2）、D2に＝SIN(B2)の関数式を書くによって値が得られます（図の表）。

cosπ+isinπが-1（表のB6）となるのでe^iπ＋１=0が得られることとなります。

さて、エクセルは複素数の計算も瞬時にしてくれます。

cosθを実部,isinθを虚部としてオイラーの公式の左辺を計算してくれるのが関数COMPLEXです。
これも最初のセルに＝COMPLEX(C2,D2,”i”)をいれてドラッグします。

また複素面（図、左下）においてｚ（cosθ、isinθ）の絶対値z、｜cosθ＋isinθ｜を計算するのがIMABSという関数式です。

表のようにオイラーの公式は複素三角関数の絶対値が１となり,またもや美しい結果に出会えました。

図、右上はθ（度）を横軸にcosθと(青）isinθ（赤）、IMBASによる｜ｚ｜（紫）を作図しました。

なおこの公式を時間変化で視覚化した立体画像を利根川先生から頂きました。青線は実数成分のコサイン波、赤線は虚数成分のサイン波、緑線が左辺の指数関数の虚数乗、を表わしています。
　
なぜか私達は波模様に安堵を感じます。

＜世界は波動で満ちている！＞
太陽光も、ラジオも、携帯も電子レンジもすべて波動の恩恵ですから私たちは波の中に生きているといっても過言ではありません（本ブログ）。

物質のふるまいをシュレジンガー（1887-1961,オーストリア）は波動関数として表しました。

音の波は健康に関係が深いようです。

音楽療法やタンゴのダンス療法が欧米で盛んとなっています。脳波が変わるのでしょうか。

その認知症予防効果については、音調による交感神経と副交感神経のバランス効果と互いを支えるダンスの踊りによるオキシトシン（ホルモン）放出増大のなせる業、ともいわれています。

日本人だから「オイラはよさこい節ダイ～」も・・アリかもしれませんね。

ところで音を‘見る’ものに出来ないものでしょうか。

＜楽譜のフーリエ表記！＞
フーリエ（1768-1830,仏）は全ての波は三角関数の波成分に分けられると考えました（図、中央）。

複音ハーモニカは上と下の段ではわずか周波数が異なる音が出て、日本的で哀愁のある音色が特徴です。舌を使うといろいろなハーモニーを奏でることができ（図、右下）、舌先を動かすタンギング奏法やマンドリン奏法もあります。

佐藤秀廊先生が昭和2年の世界ハーモニカ大会に渡欧して優勝なさった時に、その日本式複音ハーモニカを聴いた外国人達はその音の複雑さに驚き、何枚の舌で演奏したのか見せろ、と口の中を覗いたそうです。

その位複雑な音を出せる素敵な楽器なのですが簡単には上達しません。正しいハーモニーになっているのかきちんと周波数成分に分析して模範との比較がモニターとして目で確認しながら練習できれば耳に障害のある方のみならずもっと多くの方に楽しんで頂けるのではないか、と思います。

演奏は自・他の脳活動が変わり脳波も脳磁場も変わるように感じます。

最近、脳磁界の微量の変化を周波数解析できるようになりました。

＜脳波や脳電磁波のフーリエ解析＞
波動は複素数の波ともいえます。

波はフーリエ変換すると複素指数関数である時系列データから複素三角関数の和に表されます。そこではオイラーの公式が役立って、波動関数が代数的に計算出来るようになるのです。

このフーリエ変換によって脳磁界波から脳磁図が得られます。

近年は精神疾患の増大が著しく診断も治療法も混迷しています。統合失調症(精神分裂病)とうつ病との区別でも困難が多々です。

神経細胞群の活動の異常を脳電磁波の異常として検出して、波成分に分けて分析すれば疾患の非侵襲的な良いマーカーです。

健常者と統合失調症、うつ病患者で脳電磁波の高速フーリエ変換を行い、α、β、δ、θ波を比較し定量的に計測しました。統合失調症とうつ病ではいくつかの脳表面部位でδ波による違いがあることが分かりました（参考の表２）。

診断がつくと治療法も適切となります。

今後、更なる精度を求めてノイズの除外方法、統計・確率の計算やパラメーターの解析法、そして周波数域の拡大などの研究が進められるとより微細な機能変化の解析が可能となることでしょう。




  

＜統計学の必修化＞
文科省は、小学校低学年からの統計学教育の必修化を定めました。

統計学的な見方や考え方で情報を処理すれば物事の関連性を把握する力や新しい仮説を創造する力が育まれる、と言うわけです。

一歩社会に出れば統計学は、企業においては在庫管理やデータのマネジメントで、そして競合や市場の分析になくてはならないものです。

嬉しいことに、手計算の苦労やどの手法が良いのか迷った‘あの頃’とは違って今では、エクセルをクリックするだけ？そして統計解析のソフトがけっこう巷に有ります。

研究や開発においてはデータのより詳細な情報を得るために分散分析（ANOVA）をした後のpost hoc testとして多重比較法が有用であることが示されました（参考　）。

＜t-検定の繰り返しはダメョ、だから多重比較法＞
2標本（群）の平均値に違いがあると言えるかどうか、を検定する方法としてt-検定がありエクセルに搭載されています（本ブログ）。
では３標本（群）以上の時にどれとどれに違いがあるのかを知るにはt-検定を繰り返せば良いのでしょうか。
これは第一の過誤と言われ補正が必要となります。

有意水準をαとしていた場合k回検定を繰り返すと1-（1-α）^kの水準にまで下がってしまいます。４群の検定なら危険確率0.05は0.265と甘くなってしまうのです。

そこでP値に補正を加えたBonferroni法やHolm法があります。

もちろんエクセルに多群解析法としての分散分析があります。しかし分散分析法はどれとどれに有意差があるかは出ません（本ブログ）。
そのブログに載せた畑と肥料における収穫のデータにおける分散分析の結果は、列と行で、すなわち行（畑間）で有意に違いがあることのみが示されてきています。

そこでpost hoc testとしての多重比較法が役立つのです。

F統計量を使う分散分析と違って、Tukey法は全てで対比較を行う多重比較法です。

そこでエクセルの二元配置の分散分析を行った先程の畑と肥料という２要因を持つデータを使ってTukey法による解析を行ってみました（図、左下に結果の一部）。
畑２，３で有意差があるといえることが分かりました。

多重比較の解析法はエクセルに入っていませんので阪大MEPHAS統計解析プログラムを使いました。
またプログラミング言語RやRコマンダーによる解析ソフトであるEZRを用いると第一種のエラーを補正したBonferonni法やHolm法が行えます。
このEZRによる解析結果からは帰無仮説の棄却は保留とするのが良いと判断されました。

Tukey法とは検出力に違いがあることが分かります。

＜ラボで役立つ統計学＞
ものごとの関連性を掌握したい、そして新たな法則性を導きたい、それを利用して人間活動を躍進させる、それがヒトの脳が持つ社会性です。

確率と統計こそが、その事象は偶然によるのではない、何か背景に潜んでいるゾー、を確かめてくれるのです。

大発見かも！

インスピレーションに思わずこころが踊ったとき、女神の微笑みは危険確率P値、0.05や0.01として確定されます。

さて研究室の実験や、治療薬の開発では、コントロール群と二群以上の他条件処理群で違いがあるかを調べることがしばしばあります。

図、右上の場合のような対照群と多群の対比較が出来る多重比較法がDunnett法です。

このデータも阪大MEPHASプログラムで解析してみました。対照群と第二群に有意差があることが分かりました。

ヒトサンプルはそれに影響を与える要因が多く個人差が大きいため、診断薬や治療薬を開発するための疾患マーカーの確定への道のりは容易ではありません、そこでもDunnettの多重解析法が有用でした。

＜統計解析が疾患メカニズムの解明と創薬、治療法を前進させる＞
統合失調症や躁うつ病、うつ病患者の死後脳の神経ステロイドの代謝産物を測定してANOVA解析とDunnett法で解析したところ代謝分子が疾患の候補分子となることが分かりました（参考）。

統合失調症患者と躁うつ病患者の死後脳の後帯状皮質、頭頂皮質においてプレグネノロン、DHEAが有意に高いと言う結果でした（上記参考のTable3）。

神経ステロイドは脳内でコレステロールから作られて、神経細胞の発達やシナプス形成に関与し、記憶や学習機能に関与していることが知られている分子です。

こうして研究者が見つけて、取ってきた分子を解析すると未知の扉が少しづつ開いていくのです。

万能な統計解析法はありません。検定をする時はデータの正規性、等分散性、標本数、群ごとの標本数が異なっていないかなど、データの性質を鑑みてそれに適した解析法を選ぶことが肝要です（図、左上）。

通常の実験室のデータ解析では正規性の検定を行うほどにはサンプル数がなく、また生物学的な現象は正規性に近いのでパラメトリック法が使われます。

明らかに正規性に従わないときはノンパラメトリック検定法が使えますが検出が下がります。

上記論文では神経ステロイドの測定値の対数を取ってパラメトリック検定が出来ました。サンプルデータの分布背景の情報が得られることも大切です。

＜外れ値がもし除けたなら・・・＞
実験データでは時に飛びぬけた値に遭遇することがあります。
これが外せれば有意差がでるのにな～、おっと、これはいけません。どんな真実が隠れているかも知れないのですから。

平均値から２σや３σ（本ブログ）外れていたら除くという場合もありますが・・・

水準値を決めて、外せるかどうかを検定できるのがスミルノフ・グラブスの検定です。エクセルで一瞬の計算で判定できます（図の右下）。

通常はＴ値を得てその基準値におけるスミルノフ・グラブス数表のαの値から判定します。

しかし表がなくてもその横の数式を使うと好きな水準値における片側Ｐ値におけるαの値が計算できます。
エクセルの関数式、T.INVを使えば、それはｔ-分布の自由度n-1,P(片側)の確率から確率変数を逆算する関数なのでTα/nが求められます。
そこでエクセルのfxの隣のセルにイコール以降、図のように書けば一瞬のうちに数表のαの値が計算されます。

図の最下端のエクセルの挿入図ではｎが10、Ｐ値を0.05とした場合です。T.INVにはP/nとｎ-1の値をいれます。Ｔ値がαより大きければ外せることになります。

何とかものを言おう、とデータを眺めて四苦八苦するよりは、最初に検定法まで見据えた実験計画を立てることで、ラクチン？統計解析がより実りある結果を導くに違いありません。

とにかく、どんなサンプルデータも一期一会、貴重な情報であることを銘記して、未知の情報を掴みましょう。




　　今年の柿の実は一回り小さいもののぎっしりと付きました。
　　
　　とて～も甘～いのでシジュウカラもメジロもスズメもヒヨドリもオンパレード。
　　
　　夏の頃からカラスの勘クロウが数を数えていました。

　　食べごろを迎えて、

　　縁側では夫と勘クロウのサル・カニ（カラス）合戦？が始まりました。
  

＜原始宇宙を作っていたヒッグス＞
モノは目で見るか、メガネか顕微鏡か、いえいえ私は心眼ょ～

先日、欧州の世界最大規模の素粒子物理学研究機関であるCERNからの新規素粒子の発見、というヒッグス粒子のニュースに世界中が沸きました。

遂に理論が現実となったのです。

目には見えないこの素粒子の検出は今世紀のビッグスリーになることでしょう。

質量を与えてモノを作ったという暗黒原始宇宙の素粒子、ヒッグスの検出はヒッグス博士が理論を提唱して以来、半世紀近く待ち望まれて来たのです。

＜質量の起源＞
ビッグバンで宇宙が出来て一秒もしないうちに宇宙はヒッグス場で満たされたそうです。
光を反射することがない素粒子だけなので暗黒の世界です。

やがて、質量がゼロであった素粒子たちは質量を得ることによって原子や分子などモノの構成要素となっていきます（図、右上）。光子は質量がないままですがーー

それにしてもバ～ン？と宇宙が始まる前の世界はどのようにシミュレートされるのでしょうか。
どうぞ３７億年より前の世界をそっと教えて下さいな～

ヒッグス粒子は、ジュネーブの地下に建設された円周２７ ｋｍの超加速装置内で、陽子の衝突によって出てくるグルーオンから生じるようです。

そしてヒッグスの破壊物のシグナルを検出して解析するのです（図、左上）。

昨年は検出のprobability（P値）が２σだったのが遂に５σがクリアーされたのです（参考、04.07.2012: Higgs within reach）。

このCERNのニュースの３シグマや５シグマの理解は本ブログでの標準偏差σやσと信頼区間の確率の関係図が役に立ちそうです。

＜シグナルかノイズかそれが問題だ---検出限界＞
研究では高い精度を得るために、実サンプルにおける繰り返し実験を行って標準偏差や分散を解析します。そして実験結果が有意であるかを確率的に判断します。

素粒子発見のクライテリアであった5シグマについてエクセルの関数を使って理解してみましょう。

値のばらつきの程度を表すグラフが確率分布です。確率分布である正規分布はデータから得た平均値μと標準偏差σで決まり、エクセルのNORMDIST関数値と散布図を使って面積が確率を示すグラフが書けました（本ブログ）。
この確率密度曲線の関数式（本ブログ）は図の中央左の式によって正規分布が標準正規分布N（0,1^2）に変換され、標準確率密度曲線とすることが出来ます。

このようにuに変換するとどんなに便利か標準化をして表とグラフを作ってみましょう。

まずエクセルを開けて図の右下表のように左端の列に-6σから6σ、すなわち標準化した場合はσが１なので-6から6を入れます。
標準正規分布の関数式
f(x) = (1/(sqrt(2*pi))*exp(-x^2/2)) （図の中央）をマイナス無限大 からxの区間で積分することで面積値が得られ、それはxがマイナス無限大からxの間の値になる確率であることを意味します。

その値は標準累積分布関数、エクセルNORM.S.DIST（尾部はTRUE）によって得られます（表、二番目の列）。
なお表一列目は標準正規分布の確率密度の値です（NORM.S.DIST、尾部はFALSE）。

出た数値（xとｆ(x)の値）をそれぞれ囲んで散布図のグラフをクリックすると自動でxとyの関係のグラフ、標準累積分布や標準正規分布が描けます（図）。

累積分布関数値（グラフの赤線）は標準正規分布（グラフの青線）の積分値ですからxが2σならその値はグラフの灰色の面積に等しい、となりますね。

信頼区間2シグマは1から桃色の２倍の面積を引いた値です（本ブログ）。
ですから1-2*(1-NORM.S.DIST)の値によって各シグマの値が得られることになりますね（図の表）。

数式バーのf(x)の横にイコール（＝）からこの計算式を書いておくだけでエクセルのオートフィル機能で連続データが自動的に得られます。最初の列のセルをクリックしておけば後は下方にドラッグするだけなのです。

計算式を書きさえすれば瞬時に計算してくれて表が出来る、エクセルのエクセラントたるところです。

昨年は2σであった実験結果が今回、世界中の研究者の総力によって5σとなった、このことはすなわち0.954499736から0.99999427（表）まで精度がアップしたことになります。
不確かさが百万分の一以下の精度が良い実験だった、ということです。

この表と図で分かるように５シグマの時には真の値から外れる確率は小さくて塗り絵は出来ませんね。

＜経営手法におけるシックスシグマ＞
シックスシグマは1980年代の日本製造業界へ導入された品質管理のコンセプトです。

6σは上の表に示されているようにP: 0.000000002、十億個に二個の不良品しか許されないことになります。
不良率を下げて製品の高品質化と顧客満足度を上げる、という精神を掲げたおかげで現実の値は別としても「モノ作り日本」の達成度に素晴らしいものがありました。

ところがどうした訳か近年の日本製品の品質は凋落傾向です。

士気の欠落や賃金の低下そして熟練した正規社員が減少したせいなのでしょうか。

どうやら現代の企業戦略としては、ひとつの製品に完璧性を求め過ぎる‘シックスシグマ’は、グローバル化が進み迅速性が第一の市場を考えると議論の余地がある、とのことです。

素粒子の世界とは違いますね・・・



  

＜要因が複数ある時の統計解析はーー＞
FTESTのFはF検定のFジャン～

というだけではないのです。

Fは統計学の父、フィッシャー（1890-1962,英）のFです。

数学と生物学を学んだフィシャーは、ロンドン郊外の農事試験場に就職しました。

広大な敷地にある質や環境が異なる畑では同じ植物でも生育が異なり、肥料の効果もはっきり攫めません。要因が沢山あって答えが出せないのです。

さてｔ-検定を使えば、２群の平均値に差があるといえるか、という検定はできます（本ブログ）。
そこでフィシャーはそれを広げて複数のグループ間の要因に違いがあるかどうか調べられないか、と探求しました。

そして群間分散/郡内分散を調べて群間に差があることが有意かどうか、がわかる検定法を発見しました。分散分析（ＡＮＯＶＡ）です。

データが左上の表のような場合は、エクセルの分析ツールの「二元配置のくり返しのない分散分析」を選びます。
次にデータを囲んで分散分析表を得ます。
有意水準を５％とするならその表のＰ値から、各畑においては有意に、状態の違いがある、と言えることがわかるのです。

すなわち分散分析は分散の比の検定を行って要因によっておこる変動が誤差内かどうかを調べているのです。


復習となりますがｔ－検定には３種類あってどれを使うかは、まずＦ検定を行うことによって、与えられた二群のデータが等分散か不等分散かを決めました。それから分析ツールの中の適切なｔ－検定を選択して解析しました。

正規分布では確率密度曲線を描くのにNORMDISTの関数値を使いました(本ブログ）。また、ｔ-検定ではTTESTの関数式よりＰ値を得ました。

さてF検定でもエクセルに関数が揃っています。
FTEST（両側確率Ｐ）やFDIST（片側確率Ｐ）、FINVという関数を使ってＦ分布上のＰ値やＦ値が求められます。

このＦ分布という分散比の確率分布を用いたＦ検定と分散分析の発見こそフィッシャーの偉業とされているものです。

＜Ｆ分布の確率密度曲線＞
ところでＦ分布という確率分布は正規分布（本ブログ）やｔ-分布（本ブログ）の確率分布と違ってそのグラフは自由度によって大きく変わり左右対称でないのが特徴です。

その確率密度を出す関数式がエクセルではアドインされていません。
そこで私はNTFDISTという関数をエクセルに組み込みました。

ここでは自由度が３と４、３と１０の値を使ってNTFDIST関数による２種類の確率密度の値を出しました。そして散布図をクリックしてＦ分布のグラフを作成しました（図の右上）。

＜品質管理と分散分析＞
分散分析は育種や研究開発などにおける実験結果の分析のみではありません。
「世界一の品質を持つ日本！」と言われるように日本製品における品質管理では統計学が力を発揮しています。

統計的品質管理に卓越するには、数々の要因の中から品質に影響をおよぼす異常原因を統計学的に見つけ出す、そしてきちんと対処する、これに尽きますね。

このように分散分析は統計的現象の原因究明やグループ間の要因解析ができるので複数の患者への薬の効果を調べる場合にもうってつけです。

要因がひとつである一元配置の分散分析の例としては、結核菌の再来を抑えるべくしてなされた下記のようなスクリーニングの研究報告があります。

＜多剤耐性結核菌を撲滅するには＞
先日も結核菌集団罹患のニュースがありました。

日本は先進国の中でとても結核罹患率が高いのです。

なぜこの現代に結核菌に脅かされるのでしょう。

戦後、結核は日本の死亡原因の第一位でしたが化学薬品のお陰で非常に減りました。

ところが中途半端な化学療法によって耐性結核菌が生じてしまったのです。対処に困難を極めています。

南アフリカでは結核やＨＩＶに効くとされる植物由来の民間薬が沢山あるそうです。しかしその科学的な検証はなされていません。

論文では２１種類のうち４つの植物で結核菌と薬剤耐性菌の増殖を抑えることが解析されました（参考）。

成分の抽出とさらなるバイオアッセイを進めて薬剤耐性菌に効く天然の成分が分かると良いですね。

なにはともあれ結核菌に冒されても薬効が得られて死なずに済むように、薬の併用や免疫力の低下を個人のレベルで防いでおくことが大切です。

日々の健康管理に勝るものは無し、です～




  

＜学徒の魂、百まで＞
今年の遅れ馳せながらの桜よりピカピカのフレッシュマンに目が注がれます。

どうぞ中学や高校とは指導法がどんなに違うか、お楽しみアレ～　？


グローバル化の速度はあらゆる分野で著しいものがあります。とはいうものの私達の脳は生まれ育った日本という環境や文化、いえ、親の背、教師の背に負う所が多分です。

ですからそう簡単には自分作りや先を読む能力は得られませんね。大波を超えるための人生に必要な技は時を越えて自分で磨くしかありません。

大波といえば危なげなユーロ圏の経済ニュースがいつもどこかに登場です。今にも私たちを飲み込みそうな大波が続いています。

ユーロ圏では新たな経済世界を目指すとともに経済のツールである通貨もカラフルなユーロ紙幣に替わりました。

かつてのドイツのマルク紙幣は確率分布曲線（本ブログ）とその発見者のガウス（1777-1855、独逸）の顔が載っている荘重なものでした。

ものごころが付いた頃からお札を使うたびにガウスと向き合うわけです。

確率的な思考に満ちた人生であることでしょうね。

＜確率密度曲線と区間推定＞
ガウスの時代の数学者達は、現実にはデータが取りきれないような母集団の特性を把握するための数学的解析法を求めて統計学を発展させました。

さて人々の身長の分布や工場製品のばらつきについて分布を調べると標本サイズを上げるほどに、得られた標本値の分布は平均値の付近に集積します。そして左右対称の釣鐘型となる正規分布という分布型に近づきます。

ガウスは母集団の特性を知るためにはほぼ３０以上の抽出サンプルがあると平均値（μ）と標準偏差（σ）を用いた関数式によってその母集団の分布曲線に近似できることを示しました。
その関数式は確率密度関数式（本ブログ）と言い、積分すると、すなわちx軸（確率変数）と曲線で囲まれた面積が１となります。

さてこの発見はどのように世の中に役立つのでしょう。

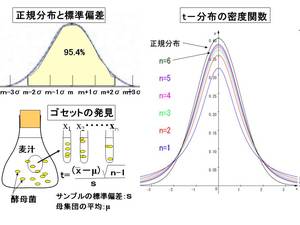図の左上が示すことはデータが±１σの範囲に入る確率は約６８．３％、±２σでは９５．４％、の確率であることを意味します。
平均値（μ）や標準偏差（σ）がどんな値であっても±１σや±２σ、±３σの範囲に入る確率は常に一定に、０．６８３、０．９５４、０．９９７となるのです。ですから平均値と標準偏差の値と目的のデータを比較すれば自ずと全体の中での特性が分かります。

しかしサンプルがヒトの場合や販売品は沢山の標本数を取って調べることが出来ません。
そこではt－分布を用いたt検定法が使われます。

＜ｔ－分布とStudent‘s t-test＞
化学と数学を学んだゴセット（1876-1937英国）はビール会社ギネスに就職しました。ギネスブックで有名ですね。

彼は醸造所で味が一定の良いビールを作るために日夜、タンクの中から酵母菌の入った麦汁を少し取り出しその菌の数を数えてタンクのビールの出来具合を推定していました（図の左下）。

製品管理のためのこの仕事において、ガウスの言うように何回も測定頻度を重ねれば一定の値により近づき、タンクの酵母菌濃度とブレが少なくすむ、ということは分かっていました、がゴセットはもっと少ない抽出実験でより正しく調べることが出来ないものか、と考えたのです。

そこで発見したのがt－分布という確率分布です。これは標本数を増やすとガウスの正規分布に近づきます（図右）。
ｔ－分布は少ない標本のみで母平均を推定することが出来るのですから凄い発見でした。

またｔ－分布を使うと２つの母集団からの２つの標本平均の差がどういう確率で有意となるか、という検定が出来ます。いわゆるStudentのｔ－テストと呼ばれる検定法です。

私たちが実験結果の報告をする時はデータをStudent のｔ-testを用いて解析した、と記し（参考）危険率が0.001（参考論文の場合）で両群のデータの平均に差があるといえる、のように確率Pがどの位小さかったかを記します。これによって読者はどれくらい危なっかしい、あるいは信憑性が高い研究結果なのかが判断出来るわけです。

Student’s t-testではunpaired　ｔ－test　としても記します。この時は対応がない独立な二つのデータにおいて平均に違いがあるかどうかを知るための検定です。

ところで　‘Student’ はゴセットのペンネームです。"学生”としたのが謙虚でいいですね～"脳研究者”などと書かない・・・

自分が出したデータを説得したい側としてはエクセル分析ツールでまずF検定を行います。そこでは比較したい両データの分散のばらつき具合を検定します。ある決められた確率で分散が等しいと判定されると、その次にｔ検定をクリックしてその中の分散が等しいと仮定した場合を、あるいは等しくない時は、等しくないと仮定した場合を選び検定結果の表と危険率P値を得ます。

なおpaired t-test(対応がある)、をエクセルで選ぶ場合は、例えば薬の投与効果を検定したい場合など、即ちbefore and afterで効果の有意差検定をしたい時です。投与前後のデータをセルに挿入後、危険率を得ます（参考、論文中図１の説明文）。

＜現代社会に必要な統計学＞
母集団の分布型がおよそ分かっている多くの生物や物理の現象や物質の特性は正規分布やt－分布の関数式によって確率論的に解析が出来ます。

ところが企業の戦略としては経済の動きや人々の購買意欲に関する全体像の解析がとても重要です。また資源の乏しい日本は他国からの物資の仕入れに関する戦略が生き残りに関わります、またIT情報の篩い操作など、これらは確率分布が決められないものですが必須のニーズとなっています。

でもこれらは次に起こることによって確率が変わりますので関数は得られないのです。

では現実社会の諸問題に統計学は太刀打ち出来ないのでしょうか。

要因が多すぎるから誰かの勘に頼るしかないのでしょうか？

現在は医療診断システムや、インターネットで受信したものがスパムメールである確率の計算などは社会数学ともいえるベイズの理論モデルを使って、不完全情報下での解析として進められています。

何はともあれ、何を調べたいのか、いかなる質と量のデータを得ればよいのか、そして分布の様式がどうなのかなど、判断が得られるような適切な分析法を進めていくことが重要です。

　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　
　　　「庭の桜はまだちらほらだね。

　　　次のブログでは桜の花がアップされるかな～」
  

＜モグラが暴れた！＞
ナ何と、庭にモグラの跡が沢山！！！

ナマズの髭が地震センサーであるようなことは有名ですがモグラのセンサーは？？？

これまでにはなかったことです。

大地震が来なければ良いが、と案じています。

そこで気象庁サイトを訪問してみました。
気象などの知識；地震について、を開けてみました。すると図、左上のような１９９６年以降の地震頻度に関するデータがありました。

エクセルは表計算ソフトとして知られています。
しかし加えて先のブログで描きましたようにいとも“エクセラント”に変数の関係をグラフなどに視覚化してくれるのです。

＜エクセル関数を使ってデータのビジュアル化＞
地震回数とマグニチュードの値を囲み散布図を描かせますと図の左下のような曲線が得られました。

さらに関数式LOGで対数値を得て両対数を取ります。直線となることが分かりました。

このことは地震の回数はマグニチュードの冪関数（累乗関数）として数式で示されることを示します。

むろんエクセルの近似曲線をクリックすれば対数値を計算しなくとも図の中に近似直線を描いて一次方程式も示してくれます。

更に関数CORRELを使うと相関係数0.94が求められ、回数とマグニチュードの相関が高いことが得られます。

図を眺めてわかるようにべき関数では小さな度数を持つ沢山の事象と大きな度数を持つ少数の事象が共存して観察されています。

このようにべき分布に従うものは正規分布と違って、平均値や標準偏差は意味がありません。

べき関数式に従うものには、地震や山火事、金融恐慌、所得の分布、商売では売れる商品と売れない商品の量と売上額、そしてウェーバー・フェヒナーの法則といわれるヒトが感じる量と刺激強度の関係があります。

メデイアによる影響が窺い知れない社会となりました。
社会的インパクト理論では、社会的インパクトの大きさIは影響発信源の数Nの関数として表され、これも　I＝ｋN^aとなる、べき関数とのことです。


そういえば、大昔習ったアレもべき関数です。

ある日、教壇で先生は「ガリレオ・ガリレイ（伊、１５６４）はピサの斜塔から同じ大きさの鉄製と木製の玉を落として同時に落ちることを実証しました」と話されました。

「私はもっと高い塔からでなければガリレオは勝てない！」と言ってしまいました。重いほうが早く落ちるというアリストテレス派の人たちは「距離が短いから」と反論できる、と思ったのです。

私は話の腰を折るイヤな子供でした・・・・・

ガリレオは医学を学びましたが数学や天文学に興味を持ち始め、実験を重ねて、ｄｓ/ｄｔ=ｇｔを見出しました。
積分するとｆ（ｔ）＝（１/2）gｔ^2+v0ｔ+s0　となりますが初期値ｔ＝０でｓ＝０です（図、右）。

従って手を離してからの距離と時間の関係はｓ＝(1/2)ｇｔ＾２となります。

重力加速度ｇは９．８１m/sec2 です。
べきの計算は関数式のＰＯＷＥＲで得てプロットします。すると図の右下のような放物線の半分が描けました。

これもべき関数である証拠に両対数を取ると直線の近似曲線が得られます。


実は、科学革命家であるガリレオが亡くなった年に、同じく偉大なる科学革命家であるニュートンが生まれています。
ニュートンはガリレオの発見した現象を数式化して物理学体系を築き上げました。

ちなみに多くの物理法則のみならず細菌の増殖などに見られる指数関数はべき関数と異なって片対数をとると直線が得られますね。

＜ＩＴ社会は自分デ情報を解析する社会＞
情報化時代では情報をどのように習得して評価し、活かすか、という情報リテラシーの向上が欠かせません。

統計局には人口、経済、労働力およそどんな情報もあります。
自分で分析できれば評論家やアナリストの言葉を鵜呑みにする必要はありませんね。

エクセル分析ツールの中の基本統計量をクリックして表を得ます。この表中の平均値や中央値、尖度、歪度、標準偏差からデータの性質を見ます。
試料の統計量から母集団の特性が推定されるのです。

次に度数分布図であるヒストグラムをクリックします。左右対称か、散らばり具合はどうかを見ます。端に偏っているとべき乗法則である可能性があります。
正規分布性はＮＯＲＭＤＩＳＴ関数で確率密度曲線を一緒に描かせると比較ができます（参考）。

身長や体重の分布やランダムに生じるような生物学的現象は平均値の上と下で度数が同じように分布します。そして標本サイズを上げれば正規分布に近づくのです。
正規分布は確率的な分布ですので保険や偏差値にも使われています。

健康管理のためにご自分のストレス分子や若返りホルモン？の変化、また運動効果の結果もどうなっているのかプロットしてみたくなった方もおられそうですね。

さて、経営の拡大を目指していろいろと売り上げアップの努力をします。が本当にその効果があったのか、そのつど検証をしていかないと意味がありません。前と後、その効果の検定は関数ＴＴＥＳＴによって危険率の値で評価が出来ます。
また製品開発の効果もＦ検定やｔ検定をクリックして平均値の検定を行なうと、より正しい判断が出来、次の戦略を導くことが出来ます。

私達が目指すことはデータをビジュアル化すること、数式解析をすること、そして自分の脳で言語化して新しい理解を得る。そして更に自分の仕事や健康のみならず社会問題の背景を認識する、ということでしょうか。

今は金融恐慌時代、幼少時からグラフ化と読み取る化の力が付いていれば、ファイナンスに長けて・・・・リスクとスリルに満ちたエクセラントな？人生が送れたかも～～


十二月の空はカラっ風が強いせいか底なしの青さ、二階まで伸びたブラジル原産の薄紫の山保呂之がとても映えます。

真冬を除いて1年中、次々と先端に花を付けます。

山にある日本原産の山保呂之には赤い実がなるそうです。



  

＜道行くひとがー＞
「これは何ですか、珍しいですね」と濃紫のフリージャを見た通りすがりのひとが声を掛けて下さいました。
おかげで、このフリージャが有りそうで無さそうな花であることを知りました。

結婚した頃、夫の実家から送られてきた食料の中にあった球根が増えたのです。

幾年も、稀有なる花とは気が付かず、本当に御見逸れ御免、です～

それにしても昨今の花屋さんのフリージャは、この濃紫は無いものの、白、黄、ショッキングピンク、薄紫、オレンジ、トルコグリーン、そして花びらの大小、白の混じり、なんとヴァラエテイなのでしょう！

＜遺伝学と統計学＞
遺伝子組み換え技術を得た現在でも、花色や穀物の品種改良はやはり昔からの交配による育種法が行われていますね。

掛け合わせ、と言えばメンデル(１８２２－１８８４、オーストリア）でしょうか。

メンデルは若い頃数学を学んだものの、教師の試験に何としてもパスできませんでした、が修道院に勤めて、裏庭で花の色、豆の形をマークに膨大な数のえんどう豆の掛け合わせを行いその結果を数値化することによって、遂に遺伝因子の存在を導きました。

その頃、ダーウイン(１８０９－１８８２、英国）が「環境に適したものが子孫を残す上で有利となる」という考えを主張し「進化は偶然が支配する変化である」と論著して社会を揺るがしていました。

そのダーウインもやはり古来の「カエルの子はカエル」という遺伝のしくみを、また表現形質の優劣のしくみを明らかにしたく植物やハトを使って猛烈に掛け合わせ実験をしていたのでした。

しかし、メンデルの数理統計のセンス、これこそがダーウインも至れなかった、遺伝の法則という大発見を後世に知らしめることを可能としたのです。

＜エクセル統計分析、平均値、中央値、ガウス分布＞
生物学や工学実験の結果のみならず、ビジネスの世界でも需要の予測、物の販売、試作品開発などにおいて、データ解析が次のステップへの根幹となります。

ところで新聞、雑誌など日本人が記したものではもっぱら平均値しか見ませんが欧米人は中央値を上手く使って説明しているのを見ます。

経済統計などはガウス（正規）分布に従わないことが多いので中央値のほうがデータの特性が得やすいのです。

平均値には極端な値（外れ値）の影響を強く受ける、ということがあります。
平均値を用いる場合は、その集団が正規分布をしていることが、絶対的な前提条件になります。

データの数が多ければ正規分布にかなり近づくはずですが、例えば、貯蓄額では数千万人が対象でも、一握りの金持ちが握り締めているので正規分布になりません。

中央値ならその値よりも大きい特性値を持つ人が全体の半分、小さい特性値を持つ人が半分という直感的に明確な意味を与えます。

ですからデータの分布に偏りや極端な数値がある場合は中央値が良さそうです。

エクセルの分析ツールを使うと統計分析の基本値が即座に表（図、基本統計量）になります。

ヒストグラムはデータの散らばり具合を視覚的に示します。

図には、私がストップウオッチで１０秒を３０回測定したときの結果を、分析ツールの中のヒストグラムを選択して入力、区切り幅を指定して書かせました。

昔、６０秒インターバルで泳ぎこんでいた私は身体が秒刻みを記憶しているかのようにバラツキ（分散や標準偏差値）は極めて小さいものでしたがーー

今回測定のエクセルの計算結果は、平均値(9.74), 中央値(9.80), 分散（0.358）, 標準偏差(0.599)などでした。

その昔、放物線やだ円などの曲線が数式で表せることを知り感激しました。

美しい曲線と言えばヴィーナスのライン、いえ正規分布曲線！！

正規分布曲線は平均値と標準偏差から求められ、エクセルの中の関数NORMDISTを使ってヒストグラムと重ねて表わすことが出来ます(図)。

手書き計算に比べ、エクセルは手間いらずで余りにexcellent！エクセルも只モノでない気がしてきます～

正規分布は臨床検査だけに留まらず最も広く用いられる分布モデルです。

健常者の多くの検査値は正規分布に近いため、そこでさまざまな検査値について平均値と標準偏差値を算出して、平均値±２標準偏差（９５％が含まれる）を正常範囲とします。

ですから確率的には健常者が２０種類の検査を受けるとどれか一つが正常範囲を外れることになりますね。

＜先行き不透明な社会でこそ確率と統計が必要？＞
この世のことは、独立でない事象が絡み合って混沌、曖昧模糊としているように感じます。

その曖昧さにつけこまれないようにするには、評価、納得できるシステム作りが大切ですね。
統計解析の検定法を用いれば、正しさ具合が推察出来ます。

今回の放射能汚染に関しては、いろいろな数字に一鬼？一憂しました。

データがどのように採取され、どのように解析されたのかが重要なのです。

私達の健康は、来たる遺伝子医療社会で個人レベルで解決されていくでしょう。

そのためには、メンデルやダーウインの苦労をはるかに超えて、個人のSNP（２月、本ブログ）データや臨床データを数値化し、確率的に効果のある情報処理科学に基づいた医療を進めていかなければなりません。