2012年07月21日
ヒッグス粒子は確率で見えた!!
<原始宇宙を作っていたヒッグス>
モノは目で見るか、メガネか顕微鏡か、いえいえ私は心眼ょ~
先日、欧州の世界最大規模の素粒子物理学研究機関であるCERNからの新規素粒子の発見、というヒッグス粒子のニュースに世界中が沸きました。
遂に理論が現実となったのです。
目には見えないこの素粒子の検出は今世紀のビッグスリーになることでしょう。
質量を与えてモノを作ったという暗黒原始宇宙の素粒子、ヒッグスの検出はヒッグス博士が理論を提唱して以来、半世紀近く待ち望まれて来たのです。
 <質量の起源>
<質量の起源>
ビッグバンで宇宙が出来て一秒もしないうちに宇宙はヒッグス場で満たされたそうです。
光を反射することがない素粒子だけなので暗黒の世界です。
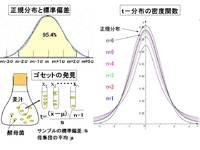
やがて、質量がゼロであった素粒子たちは質量を得ることによって原子や分子などモノの構成要素となっていきます(図、右上)。光子は質量がないままですがーー
それにしてもバ~ン?と宇宙が始まる前の世界はどのようにシミュレートされるのでしょうか。
どうぞ37億年より前の世界をそっと教えて下さいな~
ヒッグス粒子は、ジュネーブの地下に建設された円周27 kmの超加速装置内で、陽子の衝突によって出てくるグルーオンから生じるようです。
そしてヒッグスの破壊物のシグナルを検出して解析するのです(図、左上)。
昨年は検出のprobability(P値)が2σだったのが遂に5σがクリアーされたのです(参考、04.07.2012: Higgs within reach)。
このCERNのニュースの3シグマや5シグマの理解は本ブログでの標準偏差σやσと信頼区間の確率の関係図が役に立ちそうです。
<シグナルかノイズかそれが問題だ---検出限界>
研究では高い精度を得るために、実サンプルにおける繰り返し実験を行って標準偏差や分散を解析します。そして実験結果が有意であるかを確率的に判断します。
素粒子発見のクライテリアであった5シグマについてエクセルの関数を使って理解してみましょう。
値のばらつきの程度を表すグラフが確率分布です。確率分布である正規分布はデータから得た平均値μと標準偏差σで決まり、エクセルのNORMDIST関数値と散布図を使って面積が確率を示すグラフが書けました(本ブログ)。
この確率密度曲線の関数式(本ブログ)は図の中央左の式によって正規分布が標準正規分布N(0,1^2)に変換され、標準確率密度曲線とすることが出来ます。
このようにuに変換するとどんなに便利か標準化をして表とグラフを作ってみましょう。
まずエクセルを開けて図の右下表のように左端の列に-6σから6σ、すなわち標準化した場合はσが1なので-6から6を入れます。
標準正規分布の関数式
f(x) = (1/(sqrt(2*pi))*exp(-x^2/2)) (図の中央)をマイナス無限大 からxの区間で積分することで面積値が得られ、それはxがマイナス無限大からxの間の値になる確率であることを意味します。
その値は標準累積分布関数、エクセルNORM.S.DIST(尾部はTRUE)によって得られます(表、二番目の列)。
なお表一列目は標準正規分布の確率密度の値です(NORM.S.DIST、尾部はFALSE)。
出た数値(xとf(x)の値)をそれぞれ囲んで散布図のグラフをクリックすると自動でxとyの関係のグラフ、標準累積分布や標準正規分布が描けます(図)。
累積分布関数値(グラフの赤線)は標準正規分布(グラフの青線)の積分値ですからxが2σならその値はグラフの灰色の面積に等しい、となりますね。
信頼区間2シグマは1から桃色の2倍の面積を引いた値です(本ブログ)。
ですから1-2*(1-NORM.S.DIST)の値によって各シグマの値が得られることになりますね(図の表)。
数式バーのf(x)の横にイコール(=)からこの計算式を書いておくだけでエクセルのオートフィル機能で連続データが自動的に得られます。最初の列のセルをクリックしておけば後は下方にドラッグするだけなのです。
計算式を書きさえすれば瞬時に計算してくれて表が出来る、エクセルのエクセラントたるところです。
昨年は2σであった実験結果が今回、世界中の研究者の総力によって5σとなった、このことはすなわち0.954499736から0.99999427(表)まで精度がアップしたことになります。
不確かさが百万分の一以下の精度が良い実験だった、ということです。
この表と図で分かるように5シグマの時には真の値から外れる確率は小さくて塗り絵は出来ませんね。
<経営手法におけるシックスシグマ>
シックスシグマは1980年代の日本製造業界へ導入された品質管理のコンセプトです。
6σは上の表に示されているようにP: 0.000000002、十億個に二個の不良品しか許されないことになります。
不良率を下げて製品の高品質化と顧客満足度を上げる、という精神を掲げたおかげで現実の値は別としても「モノ作り日本」の達成度に素晴らしいものがありました。
ところがどうした訳か近年の日本製品の品質は凋落傾向です。
士気の欠落や賃金の低下そして熟練した正規社員が減少したせいなのでしょうか。
どうやら現代の企業戦略としては、ひとつの製品に完璧性を求め過ぎる‘シックスシグマ’は、グローバル化が進み迅速性が第一の市場を考えると議論の余地がある、とのことです。
素粒子の世界とは違いますね・・・
モノは目で見るか、メガネか顕微鏡か、いえいえ私は心眼ょ~
先日、欧州の世界最大規模の素粒子物理学研究機関であるCERNからの新規素粒子の発見、というヒッグス粒子のニュースに世界中が沸きました。
遂に理論が現実となったのです。
目には見えないこの素粒子の検出は今世紀のビッグスリーになることでしょう。
質量を与えてモノを作ったという暗黒原始宇宙の素粒子、ヒッグスの検出はヒッグス博士が理論を提唱して以来、半世紀近く待ち望まれて来たのです。
 <質量の起源>
<質量の起源>ビッグバンで宇宙が出来て一秒もしないうちに宇宙はヒッグス場で満たされたそうです。
光を反射することがない素粒子だけなので暗黒の世界です。
やがて、質量がゼロであった素粒子たちは質量を得ることによって原子や分子などモノの構成要素となっていきます(図、右上)。光子は質量がないままですがーー
それにしてもバ~ン?と宇宙が始まる前の世界はどのようにシミュレートされるのでしょうか。
どうぞ37億年より前の世界をそっと教えて下さいな~
ヒッグス粒子は、ジュネーブの地下に建設された円周27 kmの超加速装置内で、陽子の衝突によって出てくるグルーオンから生じるようです。
そしてヒッグスの破壊物のシグナルを検出して解析するのです(図、左上)。
昨年は検出のprobability(P値)が2σだったのが遂に5σがクリアーされたのです(参考、04.07.2012: Higgs within reach)。
このCERNのニュースの3シグマや5シグマの理解は本ブログでの標準偏差σやσと信頼区間の確率の関係図が役に立ちそうです。
<シグナルかノイズかそれが問題だ---検出限界>
研究では高い精度を得るために、実サンプルにおける繰り返し実験を行って標準偏差や分散を解析します。そして実験結果が有意であるかを確率的に判断します。
素粒子発見のクライテリアであった5シグマについてエクセルの関数を使って理解してみましょう。
値のばらつきの程度を表すグラフが確率分布です。確率分布である正規分布はデータから得た平均値μと標準偏差σで決まり、エクセルのNORMDIST関数値と散布図を使って面積が確率を示すグラフが書けました(本ブログ)。
この確率密度曲線の関数式(本ブログ)は図の中央左の式によって正規分布が標準正規分布N(0,1^2)に変換され、標準確率密度曲線とすることが出来ます。
このようにuに変換するとどんなに便利か標準化をして表とグラフを作ってみましょう。
まずエクセルを開けて図の右下表のように左端の列に-6σから6σ、すなわち標準化した場合はσが1なので-6から6を入れます。
標準正規分布の関数式
f(x) = (1/(sqrt(2*pi))*exp(-x^2/2)) (図の中央)をマイナス無限大 からxの区間で積分することで面積値が得られ、それはxがマイナス無限大からxの間の値になる確率であることを意味します。
その値は標準累積分布関数、エクセルNORM.S.DIST(尾部はTRUE)によって得られます(表、二番目の列)。
なお表一列目は標準正規分布の確率密度の値です(NORM.S.DIST、尾部はFALSE)。
出た数値(xとf(x)の値)をそれぞれ囲んで散布図のグラフをクリックすると自動でxとyの関係のグラフ、標準累積分布や標準正規分布が描けます(図)。
累積分布関数値(グラフの赤線)は標準正規分布(グラフの青線)の積分値ですからxが2σならその値はグラフの灰色の面積に等しい、となりますね。
信頼区間2シグマは1から桃色の2倍の面積を引いた値です(本ブログ)。
ですから1-2*(1-NORM.S.DIST)の値によって各シグマの値が得られることになりますね(図の表)。
数式バーのf(x)の横にイコール(=)からこの計算式を書いておくだけでエクセルのオートフィル機能で連続データが自動的に得られます。最初の列のセルをクリックしておけば後は下方にドラッグするだけなのです。
計算式を書きさえすれば瞬時に計算してくれて表が出来る、エクセルのエクセラントたるところです。
昨年は2σであった実験結果が今回、世界中の研究者の総力によって5σとなった、このことはすなわち0.954499736から0.99999427(表)まで精度がアップしたことになります。
不確かさが百万分の一以下の精度が良い実験だった、ということです。
この表と図で分かるように5シグマの時には真の値から外れる確率は小さくて塗り絵は出来ませんね。
<経営手法におけるシックスシグマ>
シックスシグマは1980年代の日本製造業界へ導入された品質管理のコンセプトです。
6σは上の表に示されているようにP: 0.000000002、十億個に二個の不良品しか許されないことになります。
不良率を下げて製品の高品質化と顧客満足度を上げる、という精神を掲げたおかげで現実の値は別としても「モノ作り日本」の達成度に素晴らしいものがありました。
ところがどうした訳か近年の日本製品の品質は凋落傾向です。
士気の欠落や賃金の低下そして熟練した正規社員が減少したせいなのでしょうか。
どうやら現代の企業戦略としては、ひとつの製品に完璧性を求め過ぎる‘シックスシグマ’は、グローバル化が進み迅速性が第一の市場を考えると議論の余地がある、とのことです。
素粒子の世界とは違いますね・・・
“博士が愛した数式”は、
あっと、言う間に出来る統計解析~
エクセル、FTEST,FDIST,FINVのFってナ~ニ!
ドイツでは幼い頃から確率・統計学
情報化社会では自分でデータを分析することが肝要
只モノではなかったーー
あっと、言う間に出来る統計解析~
エクセル、FTEST,FDIST,FINVのFってナ~ニ!
ドイツでは幼い頃から確率・統計学
情報化社会では自分でデータを分析することが肝要
只モノではなかったーー
Posted by 丸山 悦子 at 20:07│Comments(2)
│エクセルはエクセラント
この記事へのコメント
Most help articles on the web are inaccurate or ineechront. Not this!
Posted by Geovanny at 2014年06月04日 03:51
Dear Geovanny
It's nice to get your comment.
I teach data science and statistics, and I've found that students like touching a keyboard!
More sophisticated class may stimulate them~~It's my effort.
Etsuko
It's nice to get your comment.
I teach data science and statistics, and I've found that students like touching a keyboard!
More sophisticated class may stimulate them~~It's my effort.
Etsuko
Posted by Etsuko Maruyama at 2014年06月05日 22:06